

The equation \(Y=\beta_0+\beta_1 x\) describes this relationship in the population. We can use statistical inference (i.e., hypothesis testing) to draw conclusions about how the population of \(y\) values relates to the population of \(x\) values, based on the sample of \(x\) and \(y\) values.
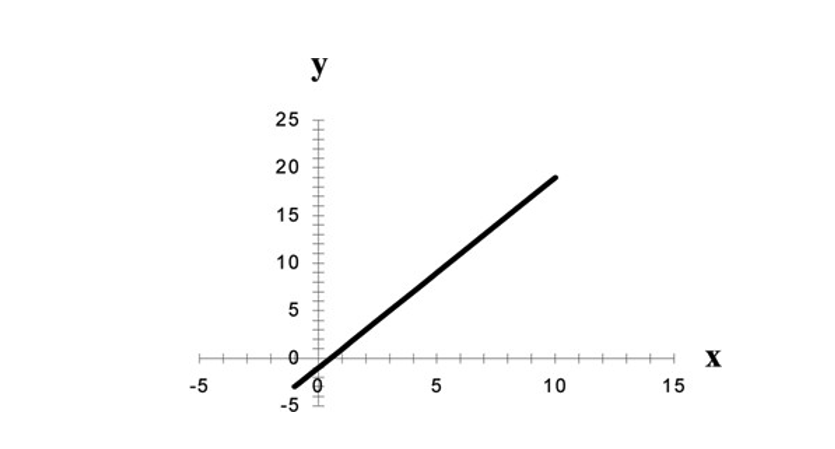
If the plot shows a pattern (e.g., bowtie or megaphone shape), then variances are not consistent and this assumption has not been met. Check this assumption by examining the scatterplot of “residuals versus fits.” The variance of the residuals should be consistent across the x-axis. Equal variances: The variance of the residuals should be consistent across all predicted values.The distribution will not be perfectly normal because we're working with sample data and there may be some sampling error, but the distribution should not be clearly skewed. You can also examine a histogram of the residuals it should be approximately normally distributed. Check this assumption by examining a normal probability plot the observations should be near the line. Normality of errors: The residuals must be approximately normally distributed.Check this assumption by examining a scatterplot of “residuals versus fits.” The correlation should be approximately 0. Independence of errors: There is not a relationship between the residuals and the predicted values.Check this assumption by examining a scatterplot of \(x\) and \(y\). Linearity: The relationship between \(x\) and y must be linear.In order to use the methods above, there are four assumptions that must be met: The \(y\) intercept is the location on the \(y\) axis where the line passes through this is the value of \(y\) when \(x\) equals 0. For every one unit increase in \(x\) the predicted value of \(y\) increases by the value of the slope. A negative slope indicates a line moving from the top left to bottom right. A positive slope indicates a line moving from the bottom left to top right. The slope is a measure of how steep the line is in algebra this is sometimes described as "change in \(y\) over change in \(x\)," or "rise over run". You may recall from an algebra class that the formula for a straight line is \(y=mx+b\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. The "linear" part is that we will be using a straight line to predict the response variable using the explanatory variable. If there are two or more explanatory variables, then multiple linear regression is necessary. The "simple" part is that we will be using only one explanatory variable. In this lesson we will be learning specifically about simple linear regression. Recall from Lesson 3, regression uses one or more explanatory variables (\(x\)) to predict one response variable (\(y\)).


 0 kommentar(er)
0 kommentar(er)
